以太坊曲线,从工作量证明到权益证明的能耗变革

想象你手中握着一把神秘的钥匙，这把钥匙能打开一个充满无限可能的新世界。在这个世界里，每一笔交易都透明无阻，每一个合约都自动执行，这就是以太坊的世界。而在这背后，有一个强大的数学工具——椭圆曲线密码学（ECC），它就像以太坊的骨骼，支撑着这个世界的运转。今天，就让我们一起揭开以太坊曲线的神秘面纱，探索这个数学世界的奇妙之旅。

什么是以太坊曲线？

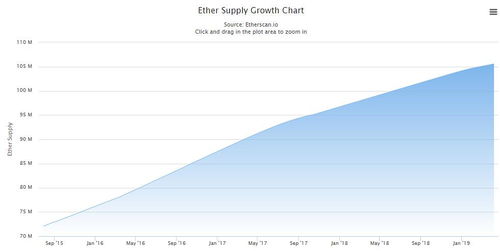
以太坊曲线，顾名思义，就是以太坊区块链中使用的椭圆曲线。简单来说，它是一种特殊的数学结构，由一系列满足特定方程的点组成。这些点在数学上有着独特的性质，使得它们在密码学中具有极高的安全性。

椭圆曲线密码学的魅力

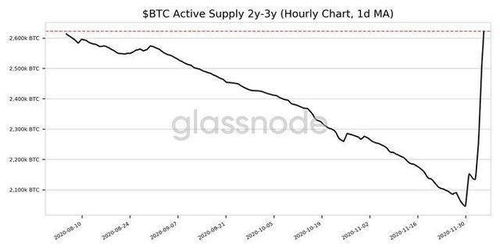
椭圆曲线密码学（ECC）是一种基于椭圆曲线数学结构的加密算法。相比于传统的加密算法，如RSA，ECC在保证安全性的同时，拥有更短的密钥长度。这意味着，使用ECC加密的数据，即使是在计算能力强大的计算机面前，也难以破解。

那么，ECC为什么这么强大呢？这得归功于椭圆曲线上的一个特殊性质——离散对数问题（ECDLP）。简单来说，ECDLP就是找到一个数，使得它与椭圆曲线上的一个点相乘后，得到另一个已知点。这个问题的难度使得ECC在密码学中具有极高的安全性。

以太坊曲线的应用

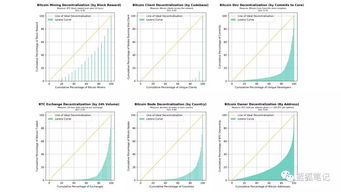
在以太坊中，椭圆曲线密码学被广泛应用于以下几个方面：

1. 地址生成：以太坊地址的生成过程，就是通过椭圆曲线密码学实现的。首先，生成一个随机的私钥，然后通过椭圆曲线数字签名算法（ECDSA）将其映射成公钥。将公钥进行哈希处理，得到一个32字节的地址。

2. 智能合约：智能合约是以太坊的核心功能之一。在智能合约中，椭圆曲线密码学被用于确保合约的执行是安全的、不可篡改的。

3. 交易验证：在以太坊网络中，交易需要经过验证才能被添加到区块链上。这个过程也依赖于椭圆曲线密码学。

以太坊曲线的安全性

以太坊曲线的安全性，主要得益于以下几个因素：

1. 数学基础：椭圆曲线密码学建立在坚实的数学基础之上，这使得它具有极高的安全性。

2. 密钥长度：相比于其他加密算法，ECC的密钥长度更短，这意味着在保证安全性的同时，可以减少计算资源的使用。

3. 抗量子计算：ECC算法对量子计算具有较好的抵抗力，这使得它在未来仍然能够保持安全性。

以太坊曲线，作为以太坊区块链的核心组成部分，为这个去中心化的世界提供了坚实的数学基础。它不仅保证了以太坊网络的安全性，还推动了区块链技术的发展。在这个充满无限可能的新世界中，椭圆曲线密码学将继续发挥重要作用，引领我们走向更加美好的未来。